La curva ipsometrica descrive l'altezza di un popolamento forestale. In letteratura è possibile trovare molte informazioni a riguardo ma quello ci cui voglio discutere in questo post è sugli aspetti pratico-applicativi per ottenere risultati attendibili (o con scarso margine di errore).
per costruire la curva ipsometrica è necessario stimare l'altezza degli alberi. Per la misura dell'altezza esistono :
- metodi diretti (approfondimento);
- metodi indiretti che si basano sulla trigonometria (approfondimento).
Quelli più utilizzati sono i metodi indiretti che si avvalgono di strumenti più o meno avanzati, ipsometri, per la misurazione dell'altezza fra cui il più preciso è il Vertex.
La curva ipsometrica è fondamentale per avere una stima volumetrica accurata, questo perchè le moderne equazioni per il calcolo della biomassa si basano su due parametri: 1) il diametro che viene misurato con cavalletto dendrometrico e 2) l'altezza (leggi il mio post "Nuove equazioni di biomassa" per approfondire)
Un metodo che consente di ottenere risultati attendibili (che uso per le mie campagne di rilievo) prevede la misurazione del 30% del numero delle piante presenti all'interno dellla AdS.
Una volta noto il numero di piante all'interno dell'AdS questo viene moltiplicato per 0.3, il numero ottenuto è il numero delle altezze che dobbiamo misurare. Es.: se all'interno dell'AdS ho contato 100 piante allora 100*0.3 = 30. Dovrò misurare l'altezza di 30 piante.
Per ogni pianta misurata è necessario conoscere il diametro, misurare l'altezza senza sapere il diametro della pianta misurata non serve a nulla! Quindi è necessario predisporre un foglio di rilievo in cui viene riportato l'altezza della pianta misurata ed il diametro misurato a petto d'uomo della pianta stessa.
E' fondamentale misurare le altezze distribuendole dalla pianta più bassa a quella più alta (se le cime sono visibili) o dalla pianta diametricamente più piccola a quella più grande.
Cose da non fare:
a) misurare sole le piante più grosse/alte;
b) misurare solo le piante più piccole/basse;
c) misurare solo le piante di diametro medio;
d) misurare poche altezze.
Arrivati a questo punto abbiamo raccolto i dati necessari che devono essere digitalizzati in un foglio di calcolo (Excel, ma anche Open Office) per stimare l'altezza compensata. Con il foglio di calcolo è possibile costruire un grafico di dispersione (scatter-plot) con in ascissa (x) il diametro [cm] ed in ordinata (y) l'altezza [m]. Il grafico di dispersione serve per visualizzare l'altezza in funzione del diametro e per poter trovare una funzione matematica di correlazione fra le due variabili. Una volta trovata la funzione che meglio descrive la correlazione basterà utilizzare i coefficienti e il diametro per ottnere l'altezza compensata.
I moderni fogli di calcolo consentono di trovare la migliore funzione ed indicarci la bontà della stima della relazione stessa. Nel caso dell'ipsometria la curva che, nella maggior parte dei casi, descrive meglio il fenomeno dell'altezza delgi alberi in funzione del diametro è quella ottenuta tramite la funzione logaritmica (LOG).
Di seguito riporto alcune informazioni aggiuntive per i più curiosi che potranno approfondire sul web le argomentazioni della funzione logaritmica.
Tratto da Wikipedia
Si definisce logaritmo in base a di un numero x l'esponente da dare ad a per ottenere x (x viene chiamato argomento del logaritmo). In altre parole, se
Nell'equazione: y = logax y è la risposta alla domanda "A quale numero bisogna elevare a per ottenere x?".
Per essere definito, la base a deve essere un numero positivo reale diverso da 1, e x deve essere un numero reale positivo. Queste ipotesi sono necessarie per fare in modo che il logaritmo esista e sia unico. Infatti:
- Se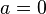
e 
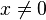, non esistono 
tali che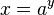 
- Se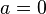 e 
, ne esistono infiniti.
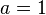- Se
e 
, non esistono .
(Non esiste nessun numero – a parte 1 stesso – che possa essere
ottenuto attraverso una potenza di 1. Infatti 1 elevato a qualunque
numero dà sempre uno).
- Se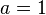 e 
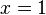, ne esistono infiniti. (Possiamo elevare 1 a qualsiasi numero ma otterremo sempre 1).
- Se
, l'elevamento a potenza 
non è definito per tutti i numeri reali (può essere definito solo sui naturali e in generale sui razionali esprimibili con una frazione con denominatore dispari).
- Il risultato di un elevamento a potenza (di un numero positivo, per l'osservazione precedente) è un numero positivo, quindi deve essere
.
Una volta costruita la curva sarà possibile calcolare l'altezza media del popolamento. L'altezza media è l'altezza della pianta di area basimetrica media (a cui corrisponde un diametro) letta sulla curva ipsometrica (altezze compensate).
Il passaggio successivo sarà quello di raccolgiere altri dati oltre che il diametro in modo da poter costruire curve ispometriche per specie, classe diametrica, per fascia altimetrica, stato della pianta viva/morta/malata ecc. ecc..
Di seguito alcune curve ipsometriche della tenuta di San Rossore scaricabili dal web.
per costruire la curva ipsometrica è necessario stimare l'altezza degli alberi. Per la misura dell'altezza esistono :
- metodi diretti (approfondimento);
- metodi indiretti che si basano sulla trigonometria (approfondimento).
Quelli più utilizzati sono i metodi indiretti che si avvalgono di strumenti più o meno avanzati, ipsometri, per la misurazione dell'altezza fra cui il più preciso è il Vertex.
La curva ipsometrica è fondamentale per avere una stima volumetrica accurata, questo perchè le moderne equazioni per il calcolo della biomassa si basano su due parametri: 1) il diametro che viene misurato con cavalletto dendrometrico e 2) l'altezza (leggi il mio post "Nuove equazioni di biomassa" per approfondire)
Un metodo che consente di ottenere risultati attendibili (che uso per le mie campagne di rilievo) prevede la misurazione del 30% del numero delle piante presenti all'interno dellla AdS.
Una volta noto il numero di piante all'interno dell'AdS questo viene moltiplicato per 0.3, il numero ottenuto è il numero delle altezze che dobbiamo misurare. Es.: se all'interno dell'AdS ho contato 100 piante allora 100*0.3 = 30. Dovrò misurare l'altezza di 30 piante.
Per ogni pianta misurata è necessario conoscere il diametro, misurare l'altezza senza sapere il diametro della pianta misurata non serve a nulla! Quindi è necessario predisporre un foglio di rilievo in cui viene riportato l'altezza della pianta misurata ed il diametro misurato a petto d'uomo della pianta stessa.
E' fondamentale misurare le altezze distribuendole dalla pianta più bassa a quella più alta (se le cime sono visibili) o dalla pianta diametricamente più piccola a quella più grande.
Cose da non fare:
a) misurare sole le piante più grosse/alte;
b) misurare solo le piante più piccole/basse;
c) misurare solo le piante di diametro medio;
d) misurare poche altezze.
Arrivati a questo punto abbiamo raccolto i dati necessari che devono essere digitalizzati in un foglio di calcolo (Excel, ma anche Open Office) per stimare l'altezza compensata. Con il foglio di calcolo è possibile costruire un grafico di dispersione (scatter-plot) con in ascissa (x) il diametro [cm] ed in ordinata (y) l'altezza [m]. Il grafico di dispersione serve per visualizzare l'altezza in funzione del diametro e per poter trovare una funzione matematica di correlazione fra le due variabili. Una volta trovata la funzione che meglio descrive la correlazione basterà utilizzare i coefficienti e il diametro per ottnere l'altezza compensata.
I moderni fogli di calcolo consentono di trovare la migliore funzione ed indicarci la bontà della stima della relazione stessa. Nel caso dell'ipsometria la curva che, nella maggior parte dei casi, descrive meglio il fenomeno dell'altezza delgi alberi in funzione del diametro è quella ottenuta tramite la funzione logaritmica (LOG).
 |
| Funzione logaritmica (fonte internet). |
Di seguito riporto alcune informazioni aggiuntive per i più curiosi che potranno approfondire sul web le argomentazioni della funzione logaritmica.
Tratto da Wikipedia
Si definisce logaritmo in base a di un numero x l'esponente da dare ad a per ottenere x (x viene chiamato argomento del logaritmo). In altre parole, se
Nell'equazione: y = logax y è la risposta alla domanda "A quale numero bisogna elevare a per ottenere x?".
Per essere definito, la base a deve essere un numero positivo reale diverso da 1, e x deve essere un numero reale positivo. Queste ipotesi sono necessarie per fare in modo che il logaritmo esista e sia unico. Infatti:
- Se
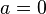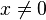e , non esistono tali che 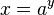- Se
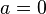e , ne esistono infiniti. - S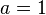e
e , non esistono .
(Non esiste nessun numero – a parte 1 stesso – che possa essere
ottenuto attraverso una potenza di 1. Infatti 1 elevato a qualunque
numero dà sempre uno). - Se
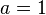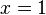e , ne esistono infiniti. (Possiamo elevare 1 a qualsiasi numero ma otterremo sempre 1). - Se
, l'elevamento a potenza non è definito per tutti i numeri reali (può essere definito solo sui naturali e in generale sui razionali esprimibili con una frazione con denominatore dispari). - Il risultato di un elevamento a potenza (di un numero positivo, per l'osservazione precedente) è un numero positivo, quindi deve essere
.Una volta costruita la curva sarà possibile calcolare l'altezza media del popolamento. L'altezza media è l'altezza della pianta di area basimetrica media (a cui corrisponde un diametro) letta sulla curva ipsometrica (altezze compensate).
Il passaggio successivo sarà quello di raccolgiere altri dati oltre che il diametro in modo da poter costruire curve ispometriche per specie, classe diametrica, per fascia altimetrica, stato della pianta viva/morta/malata ecc. ecc..
Di seguito alcune curve ipsometriche della tenuta di San Rossore scaricabili dal web.
Commenti